맨위로가기

열역학 법칙

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

열역학 법칙은 열과 에너지의 상호작용을 설명하는 기본 원리들을 포괄하며, 0법칙, 1법칙, 2법칙, 3법칙, 그리고 옹사거 상호 관계로 구성된다. 열역학 제0법칙은 열 평형 상태를 정의하며, 온도를 경험적 매개변수로 규정하는 기초를 제공한다. 열역학 제1법칙은 에너지 보존 법칙으로, 고립계의 총 에너지는 일정하며, 에너지는 형태만 변환될 뿐 생성되거나 소멸되지 않는다는 것을 의미한다. 열역학 제2법칙은 자연 과정의 비가역성을 나타내며, 엔트로피의 개념을 도입하여 열의 흐름과 무질서의 증가를 설명한다. 열역학 제3법칙은 절대 영도에서 엔트로피가 일정한 값에 접근함을 나타낸다. 옹사거 상호 관계는 비평형 열역학에서 열역학적 흐름과 힘 사이의 관계를 설명하며, 열역학의 네 번째 법칙으로 간주된다. 이러한 법칙들은 다양한 과학 및 공학 분야에서 널리 활용된다.

더 읽어볼만한 페이지

  • 열역학 법칙 - 열역학 제1법칙
    열역학 제1법칙은 닫힌 계의 내부 에너지 변화가 계가 흡수한 열과 계가 한 일의 차이와 같다는 에너지 보존 법칙의 한 측면이다.
  • 열역학 법칙 - 열역학 제2법칙
    열역학 제2법칙은 외부 도움 없이 저온에서 고온으로 열이 이동하거나 열에너지가 다른 효과 없이 모두 일로 전환되는 순환 과정이 불가능하며, 에너지 흐름의 방향성과 비가역성을 설명하는 클라우지우스 법칙, 켈빈 법칙, 엔트로피 증가 법칙 등으로 표현될 수 있다.
  • 과학 법칙 - 만유인력의 법칙
    만유인력의 법칙은 모든 질량을 가진 물체들이 서로를 끌어당기는 힘에 대한 법칙으로, 뉴턴은 질량에 비례하고 거리의 제곱에 반비례한다는 것을 제시했으며, 케플러의 행성 운동 법칙을 설명하고 뉴턴 역학의 기초가 되었으나, 일반 상대성 이론이 등장하면서 저중력 한계로 여겨진다.
  • 과학 법칙 - 보일의 법칙
    보일의 법칙은 온도와 질량이 일정할 때 기체의 압력과 부피가 반비례한다는 법칙으로, 로버트 보일이 발견했으며, 수학적으로 PV = k로 표현된다.
  • 화학에 관한 - 칼륨
    칼륨은 은백색의 무른 알칼리 금속으로 반응성이 매우 높고 생물학적으로 중요한 전해질이며, 비료 생산을 비롯한 다양한 산업 분야에서 활용되지만 물과의 격렬한 반응 및 폭발성 과산화물 생성 가능성으로 취급 시 주의가 필요하며, 자연계에 세 가지 동위원소로 존재한다.
  • 화학에 관한 - 파울리 배타 원리
    파울리 배타 원리는 1925년 볼프강 파울리가 제시한 양자역학 원리로, 동일한 페르미온은 동일한 양자 상태에 존재할 수 없으며, 원자의 전자 배치, 화학 결합, 천체 특성 등을 설명하는 데 중요한 역할을 한다.
열역학 법칙
개요
이름열역학 법칙
분야열역학
핵심 내용에너지 보존 법칙
엔트로피 증가 법칙
절대 영도
열역학 제0법칙
내용열역학적 평형 상태의 추이성
설명만약 두 계가 각각 세 번째 계와 열역학적 평형 상태에 있다면, 이 두 계는 서로 열역학적 평형 상태에 있다.
열역학 제1법칙
내용에너지 보존 법칙
설명고립계의 에너지는 일정하다. 에너지는 한 형태에서 다른 형태로 변환될 수 있지만, 생성되거나 소멸될 수 없다.
수식ΔU = Q - W (ΔU는 내부 에너지 변화, Q는 가해진 열, W는 계가 한 일)
열역학 제2법칙
내용엔트로피 증가 법칙
설명고립계의 엔트로피는 감소하지 않는다. 자연적인 과정은 엔트로피가 증가하는 방향으로 진행된다.
수식ΔS ≥ 0 (ΔS는 엔트로피 변화)
열역학 제3법칙
내용절대 영도에서의 엔트로피
설명절대 영도(0 K)에서 완전한 결정의 엔트로피는 0이다. 절대 영도에 도달하는 것은 불가능하다.
역사적 맥락
기원19세기, 니콜라 레오나르 사디 카르노, 루돌프 클라우지우스, 윌리엄 톰슨 (켈빈 경) 등의 연구에서 비롯됨
중요성엔진, 냉장고, 열펌프 등 열역학적 시스템의 효율과 작동 원리 이해에 필수적
응용 분야
에너지 시스템발전소, 내연 기관, 냉동 공학
화학화학 반응, 상평형, 용액
재료 과학재료의 안정성, 상변태
우주론우주의 열적 진화, 블랙홀 열역학
추가 정보
관련 개념통계역학
화학 열역학
비가역 과정
참고 문헌Callen, Herbert B. (1985). *Thermodynamics and an Introduction to Thermostatistics*. (2nd ed.). New York: John Wiley & Sons.
Çengel, Yunus A.; Boles, Michael A. (2002). *Thermodynamics: An Engineering Approach*. (4th ed.). New York: McGraw-Hill.
Fermi, Enrico (1936). *Thermodynamics*. New York: Prentice Hall.

2. 역사

열역학의 역사는 근본적으로 물리학의 역사와 화학의 역사와 밀접하게 얽혀 있으며, 고대 시대의 열 이론으로 거슬러 올라간다. 19세기와 20세기 초에 걸쳐 열역학 법칙들이 정립되었다. 사디 카르노는 1824년 그의 저서 ''불의 동력에 대한 고찰''에서 열역학의 첫 번째 원리(후에 열역학 제2법칙으로 불림)를 제시하였다. 1860년까지 루돌프 클라우지우스와 윌리엄 톰슨 등의 과학자들에 의해 현재의 열역학 제1법칙과 열역학 제2법칙이 확립되었다. 이후, 발터 네른스트가 1906년부터 1912년까지 네른스트의 정리(또는 네른스트의 공준)를 공식화하여 현재의 열역학 제3법칙이 되었다. 20세기 동안 법칙들의 번호가 통용되었지만, 여러 교과서에서 서로 다른 번호를 부여하기도 했다. 어떤 분야에서는 제2법칙이 열기관의 효율성만을 다루는 것으로, 엔트로피 증가는 제3법칙으로 간주되기도 했다. 이후, 절대 온도에 대한 일관적인 정의를 위해 열역학 제0법칙이 추가되었다.

3. 열역학 법칙

열역학 법칙은 계들 간의 일과 열의 변환을 다루는 고전적인 이론이다. 열역학은 열적 평형 상태에 있는 각 계의 상태를 중심으로 기술하며, 특히 열적 평형 조건에서는 계를 거시적인 변수로 쉽게 다룰 수 있다.

열역학 법칙은 19세기와 20세기 초에 걸쳐 발전했다. 1824년 사디 카르노가 ''불의 동력에 대한 고찰''에서 열역학 제2법칙을 처음 공식화했고, 1860년까지 루돌프 클라우지우스와 윌리엄 톰슨 등의 연구를 통해 현재 제1법칙과 제2법칙이 확립되었다. 이후 1906년부터 1912년까지 발터 네른스트에 의해 네른스트의 정리(또는 네른스트의 공준)가 공식화되어 제3법칙으로 알려졌다.

각 법칙은 다음과 같다.


  • 열역학 제0법칙: 두 계가 다른 세 번째 계와 열적 평형 상태에 있으면 서로 열적 평형 상태에 있다는 법칙이다.
  • 열역학 제1법칙: 고립된 계의 에너지는 일정하며, 에너지는 다른 형태로 전환될 수 있지만 생성되거나 파괴될 수 없다는 법칙이다.
  • 열역학 제2법칙: 고립 계의 엔트로피가 열적 평형 상태에 있지 않다면 엔트로피는 계속 증가해야 한다는 법칙이다.
  • 열역학 제3법칙: 온도가 0으로 접근하면 계의 엔트로피가 일정한 값을 가진다는 법칙이다.


옹사거 상호 관계는 열역학의 네 번째 법칙으로 간주되기도 한다.

3. 1. 열역학 제0법칙

열역학 제0법칙은 열역학적 시스템에서 온도를 경험적 매개변수로 규정하는 기초를 제공하며, 열 평형 상태에 있는 여러 물체의 온도 사이의 전이 관계를 확립한다. 이 법칙은 다음과 같이 표현할 수 있다.

이 법칙은 만약 두 개의 계가 다른 세 번째 계와 열적 평형 상태에 있으면 이 두 개의 계는 반드시 서로에 대해 열적 평형 상태이어야 한다는 것이다.[4] 이는 온도를 정의하는 하나의 방법이다.

:A \sim B \wedge B \sim C \Rightarrow A \sim C

이 버전의 법칙은 가장 일반적으로 언급되는 버전 중 하나이지만, "제0법칙"으로 명명된 다양한 진술 중 하나일 뿐이다. 일부 진술은 더 나아가 온도가 1차원적이며 개념적으로 더 차가운 것부터 더 뜨거운 것까지 실수의 수열로 물체를 배열할 수 있다는 중요한 물리적 사실을 제공한다.[5][6][7]

온도와 열 평형의 이러한 개념은 열역학의 기본이며 19세기에 명확하게 언급되었다. '제0법칙'이라는 이름은 제1, 제2, 제3법칙이 널리 알려진 후 한참 뒤인 1930년대에 랄프 H. 파울러에 의해 만들어졌다. 이 법칙은 엔트로피, 즉 공액 변수를 참조하지 않고 온도를 순환적이지 않은 방식으로 정의할 수 있게 해준다. 이러한 온도 정의를 '경험적'이라고 한다.[8][9][10][11][12][13]

3. 2. 열역학 제1법칙

열역학 제1법칙은 열역학적 과정에 적용된 에너지 보존 법칙의 한 형태이다. 일반적으로 에너지 보존 법칙은 고립계의 총 에너지는 일정하다는 것을 의미한다. 에너지는 한 형태에서 다른 형태로 변환될 수 있지만 생성되거나 파괴될 수는 없다.

열역학 제1법칙은 몇 가지 원리를 포함한다.

  • 에너지 보존 법칙은 에너지가 생성되거나 파괴될 수 없고, 형태만 바뀔 수 있다고 말한다. 이 법칙의 특정한 결과는 고립계의 총 에너지가 변하지 않는다는 것이다.
  • 내부 에너지의 개념과 온도의 관계. 계가 특정 온도를 가지면, 총 에너지에는 운동 에너지 (계 전체의 움직임에 의한 에너지), 위치 에너지 (외부에서 가해지는 힘장에 의해 발생하는 에너지), 내부 에너지의 세 가지 뚜렷한 구성 요소가 있다. 내부 에너지 개념의 확립은 열역학 제1법칙을 더 일반적인 에너지 보존 법칙과 구별한다.

:E_{\rm total} = KE_{\rm system} + PE_{\rm system} + U_{\rm system}

  • 일은 계와 주변 사이에서 작용하는 거시적인 기계적 힘으로 설명될 수 있는 방식으로 계로 또는 계에서 에너지를 전달하는 과정이다. 계가 한 일은 전체 운동 에너지, 전체 위치 에너지 또는 내부 에너지에서 발생할 수 있다. 예를 들어, 기계(계의 일부가 아님)가 계를 위로 들어 올릴 때, 일부 에너지가 기계에서 계로 전달된다. 계에 일이 가해짐에 따라 계의 에너지가 증가하고, 이 경우 계의 에너지 증가는 계의 중력 위치 에너지 증가로 나타난다.
  • 물질이 계로 이동할 때, 그와 관련된 내부 에너지와 위치 에너지가 새로운 결합된 계로 전달된다.

:\left( u \,\Delta M \right)_{\rm in} = \Delta U_{\rm system}

:여기서 u는 주변에서 측정된 전달된 물질의 단위 질량당 내부 에너지를 나타내고, \Delta M는 전달된 질량을 나타낸다.

  • 열의 흐름은 에너지 전달의 한 형태이다. 열 전달은 일이나 물질의 전달이 아닌 다른 방식으로 계로 또는 계에서 에너지를 이동시키는 자연스러운 과정이다. 투열벽 계에서 내부 에너지는 열로서의 에너지 전달에 의해서만 변경될 수 있다.

:\Delta U_{\rm system}=Q.

이러한 원리를 결합하면 열역학 제1법칙의 전통적인 한 가지 설명이 나온다. 즉, 동일한 양의 에너지 입력을 하지 않고 영구적으로 일을 출력하는 기계를 만들 수 없다. 또는 간단히 말해서, 제1종 영구 기관은 불가능하다.

열역학적 의미로, 내부 에너지의 변화는 공급된 열에 일을 빼준 값과 동일하다.

:\mathrm{d}U=\delta Q-\delta W\,

3. 3. 열역학 제2법칙

어떤 고립 계의 엔트로피가 열적 평형 상태에 있지 않다면 엔트로피는 계속 증가해야 한다. 닫힌 계는 점차 열적 평형 상태에 도달하도록 변화한다. 즉 엔트로피를 최대화하기 위해 계속 변화한다. 이 법칙은 제2종 영구 기관이 불가능함을 보인다.[1]

열역학 제2법칙은 자연 과정의 비가역성을 나타내며, 많은 경우 자연 과정이 물질과 에너지, 특히 온도의 공간적 균질성을 향하는 경향을 나타낸다. 이 법칙은 다양하고 흥미로우며 중요한 방식으로 공식화될 수 있다. 가장 간단한 형태 중 하나는 클라우지우스 명제로, 열은 저온의 물체에서 고온의 물체로 자발적으로 전달되지 않는다는 것이다.[1]

이 법칙은 엔트로피라는 열역학적 시스템의 양의 존재를 암시한다.[1]

제2법칙은 가역 과정과 비가역 과정 모두에 적용된다. 제2법칙에 따르면, 가역 열 전달에서 전달된 열의 요소 \delta Q는 시스템과 열의 원천 또는 목적지 모두의 온도(T)와 시스템의 공액 변수인 엔트로피(S)의 증가분(dS)의 곱이다.[1]

가역 과정은 유용하고 편리한 이론적 극한 경우이지만, 모든 자연 과정은 비가역적이다. 이러한 비가역성의 주요 예는 전도 또는 복사에 의한 열 전달이다. 두 물체의 온도가 처음에는 서로 달랐지만 직접적인 열적 연결이 이루어지면 열이 즉시 고온의 물체에서 저온의 물체로 자발적으로 흐른다는 것은 엔트로피 개념이 발견되기 오래 전에 알려졌다.[1]

엔트로피는 거시적 상태만 알려져 있을 때 시스템의 운동과 구성에 대한 미시적 세부 사항을 나타내는 물리적 척도로 볼 수도 있다. 이러한 세부 사항은 종종 미시적 또는 분자적 규모의 ''무질서''로, 그리고 드물게 ''에너지 분산''으로 언급된다. 시스템의 주어진 두 개의 거시적으로 지정된 상태에 대해, '두 상태 간 정보 엔트로피의 차이'라고 하는 수학적으로 정의된 양이 있다. 이는 다른 거시적으로 지정된 상태의 거시적 사양이 주어졌을 때, 거시적으로 지정된 하나의 상태를 지정하기 위해 얼마나 많은 추가 미시적 물리적 정보가 필요한지를 정의한다. 종종 명시적으로 언급되기보다는 미리 존재한다고 가정할 수 있는 편리하게 선택된 기준 상태이다. 자연 과정의 최종 조건은 항상 과정의 초기 조건의 거시적 사양에서 완전히 정확하게 예측할 수 없는 미시적으로 지정 가능한 효과를 포함한다. 이것이 자연 과정에서 엔트로피가 증가하는 이유이다. 증가는 초기 거시적으로 지정된 상태를 최종 거시적으로 지정된 상태와 구별하기 위해 얼마나 많은 추가 미시적 정보가 필요한지를 알려준다.[14] 마찬가지로 열역학적 과정에서 에너지가 확산된다.

3. 4. 열역학 제3법칙

열역학 제3법칙은 온도가 절대 영도에 접근함에 따라 그 엔트로피가 일정한 값에 접근한다는 법칙이다.[2]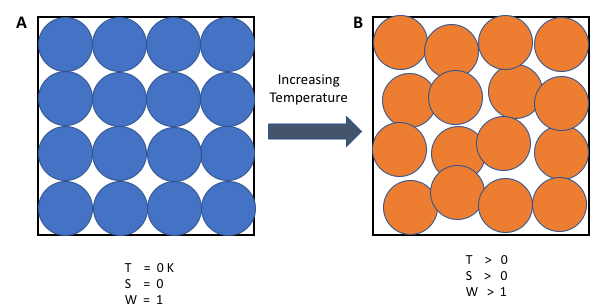

a) 절대 영도에서 계는 단 하나의 미시상태만 가질 수 있다. b) 절대 영도보다 높은 온도에서는 원자 진동으로 인해 여러 미시상태가 가능하다 (그림에서 과장됨).


절대 영도에서 계는 최소 열에너지를 갖는 바닥 상태에 있다. 이때 엔트로피의 상수 값(반드시 0일 필요는 없음)은 계의 잔여 엔트로피라고 부른다. 유리와 같은 비결정성 고체를 제외하면, 계의 잔여 엔트로피는 보통 0에 가깝다.[2] 하지만 이 값은 계가 유일한 바닥 상태를 가질 때만 0이 된다(최소 열에너지를 갖는 상태가 단 하나의 구성, 즉 미시상태만 갖는 경우). 미시상태는 각 상태가 발생할 확률이 동일하다는 가정 하에, 미시상태가 적은 거시적 상태일수록 발생 가능성이 낮다는 점을 이용하여 특정 상태에 있는 계의 확률을 설명하는 데 사용된다. 볼츠만 원리에 따르면, 엔트로피는 가능한 미시상태의 수와 관련이 있다.

:S = k_{\mathrm B}\, \mathrm{ln}\, \Omega

여기서 ''S''는 계의 엔트로피, ''k''B는 볼츠만 상수, ''Ω''는 미시상태의 수이다. 절대 영도에서는 가능한 미시상태가 하나뿐이며(''Ω'' = 1, 순수한 물질의 경우 모든 원자가 동일하므로 모든 배열이 동일하며 단 하나의 조합만 존재한다), \ln(1)=0이다.

3. 5. 옹사거 상호 관계

옹사거 상호 관계는 열역학의 네 번째 법칙으로 여겨져 왔다.[15][16][17] 이는 비평형 열역학에서 열역학적 흐름과 힘 사이의 관계를 설명하며, 열역학적 변수가 국소 평형 상태에서 국소적으로 정의될 수 있다는 가정을 따른다. 이러한 관계는 미시적 가역성의 원칙에 따라 통계 역학으로부터 유도된다(외부 자기장이 없을 때). 일련의 광범위 변수 ''X'' (에너지, 질량, 엔트로피, 입자 수 등)와 열역학적 힘 ''F'' (온도 및 압력과 같은 관련 고유 매개변수와 관련)가 주어지면, 옹사거 정리는 다음과 같이 말한다.[16]

:\frac{\mathrm dJ_k }{ \mathrm{d} F_i } \bigg|_{F_i=0} ~=~ \frac{ \mathrm{d} J_i }{ \mathrm{d} F_k } \bigg|_{F_k=0}

여기서 ''i'', ''k''는 1, 2, 3, ...이며 모든 매개변수와 관련된 힘을 나타내며,

:J_i = \frac{\mathrm dX_i }{ \mathrm dt }

는 열역학적 흐름이라고 불린다.

4. 열역학 법칙의 응용

열역학 법칙은 증기 기관, 내연 기관, 냉장고, 에어컨 등 다양한 열기관 및 열역학적 시스템의 작동 원리를 설명하고 효율을 분석하는 데 사용된다. 또한, 화학 반응, 상변화, 용액의 성질 등 화학적 현상을 이해하고 예측하는 데에도 활용된다. 열역학 법칙은 에너지 변환, 신소재 개발, 환경 문제 해결 등 다양한 분야에서 폭넓게 응용되고 있으며, 지속 가능한 발전과 인류의 삶의 질 향상에 기여하고 있다.

참조

[1] 서적 Thermodynamics. An Advanced Treatment for Chemists and Physicists North Holland, Amsterdam 1985
[2] 서적 Thermal Physics W.H. Freeman, San Francisco 1980
[3] 서적 Equilibrium Thermodynamics McGraw-Hill, London 1968
[4] 문서 Guggenheim 1985
[5] 서적 Thermodynamics and Statistical Mechanics Academic Press, New York 1951/1955
[6] 간행물 The concepts of thermodynamics North-Holland, Amsterdam 1978
[7] 간행물 'An Outline of Thermodynamical Structure' Springer, Berlin 1986
[8] 서적 Equilibrium Thermodynamics Cambridge University Press 1968/1983
[9] 서적 A Survey of Thermodynamics American Institute of Physics Press, New York 1994
[10] 서적 The Concepts of Classical Thermodynamics Cambridge University Press, London 1966
[11] 서적 Classical Thermodynamics Wiley–Interscience, London 1970
[12] 서적 Elements of Classical Thermodynamics for Advanced Students of Physics Cambridge University Press, Cambridge 1957/1966
[13] 서적 Thermodynamics and Statistical Mechanics Cambridge University Press, London 1966
[14] 서적 A Farewell to Entropy: Statistical Thermodynamics Based on Information World Scientific, New Jersey 2008
[15] 논문 Simplified transport theory for electrolyte solutions American Chemical Society (ACS) 1974
[16] 서적 Quantum thermodynamics : an introduction to the thermodynamics of quantum information https://www.worldcat[...] Morgan & Claypool Publishers 2019
[17] 백과사전 Lars Onsager – American chemist https://www.britanni[...] 2021-03-10


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com